第8週もスライド資料の説明から入った。
講義最後に小テストがあったが、時間がなかったため、一緒に見ていきましょうということで、ササっとおさらい、のような感じだった。
以下、スライド資料・講義の内容をまとめる。
Sample
yi = y1, y2, ..., yn(n個のサンプリングデータ)
サンプリングの目的は母集団全体に関しての結論を引き出すこと。
サンプルのアイテムは random variables(確率変数)。
・母集団の要素はランダムに選ばれる
・確率に関して予測値がある
母集団から得られる
Yバー、Median、Mode、Proportion、Standard deviation
は標本集団からも、
yバー、median、mode、proportion、standard deviation
と得られ、小文字で表現する。
Errors
Non-sampling errors
・統計データの記録は常にエラーを含む
(処理エラー、集合エラー、誤解、誤答)
・サイズが不明だと制御するのは困難
Sampling errors
・すべてのデータを調査できない/しないという事実から発生(全体データを知らない)
・統計手法で良く推定することができる
・程度は、母集団の特徴、サンプル手順、指標のタイプ、サンプルサイズによる
Representative sample(代表標本)であることが重要(前提)。
より大きなサンプルデータであればあるほど、エラーは減少する。
Questions to be answered
どうやって適切に母集団からサンプリングするか。
Sample size
サンプルは常に有限の要素数を持つ。
大きなサンプル数の場合、サンプルから計算される特性の相当な部分が、正規分布に従う。(normally distributed)
例:
標本平均(sample mean)や標本比率(sample proportion)は正規分布(normally distributed)に従い、標準偏差(standard deviation)は従わない
Selection ratio:n / N
⇔ どれだけ大きな母集団から取られた標本か
n / N < 5%の場合、IIDとSRはそう大差がない(後述)
Sampling plans
Probability sampling procedure(確率標本抽出手順)
・標本内に含まれる各母集団要素の確立が予めわかっている
・無作為性(randomness)が客観的に保証されていなければならない
(乱数生成、無作為性開始点からの等間隔)
Non-probability sampling procedures(非確率抽出法)
・標本誤差(sampling error)のサイズを正確には決められない
Sampling procedures
Probability(確率抽出法)
Independent and identically distributed(IID):独立同一分布
Simple random(SR):単純無作為抽出法
Stratified(S):層化抽出法
Cluster:集落抽出法
Non-probability(非確率抽出法)
Quota:割り当て法
Judgmental / purposive:有意抽出法
Snowball:機縁法(雪だるま式抽出法)
Voluntary / expert:応募法
Probability(確率抽出法)
IID and SR sampling
Reverse IID sampling
新しい標本要素を選ぶとき、母集団の構成は同じ
⇔ 標本要素は独立で同一分布(IID)ランダム変数
例:クラスひとりひとりの名前が書かれた紙を帽子の中に入れて、無作為に選ぶ。⇔ 数学的に見たときには簡単でシンプルな方法
Non-reverse Simple Random(SR)sampling
非復元等確率抽出(equal probability sample without replacement)の方が一般的。
※非復元=抽出したらそれを母集団に戻さないこと
選択率が小さい場合(母集団が大きい場合)は、基本的にIIDと同じ。
※ Selection ratio n / N が十分に小さいとき、母集団へ戻そうが戻すまいが大差がない
例:N = 100万の母集団の場合、n / 1,000,000とn / 999,999は大差がない
⇔ IID抽出として取り扱う。
Stratified sampling
Stratified(S)sample(層化抽出法)
有限で、不均一な母集団の場合に使用される。
適切な基準によって、母集団は可能な限り均一な階層として分類される。
⇔ SR抽出は各階層から別々に行われる
階層内に均一性があると、同じ抽出サイズで、より正確な結果が得られる。
例:旭丘出身の年収 → 性別で層化、学卒・院卒等で層化など
Cluster sampling
Cluster sample(集落抽出法)
均一・有限の母集団の場合使用される。
SR抽出が各集団からされ、その集団が観察される。
均一性集団の場合、効率的でない。不均一性集団の場合、正確性はSR抽出と同じ。
SR抽出より安価。
Multistage sample(多段抽出法)
集団選択後、その集団から標本を抽出。
Non-probability(非確率抽出法)
母集団の代表標本だと保証されているわけではない。
標本から計算されるエラーの特質は予測できない。→ Inference is doubtful
この方法の使用理由は・・・
実行が単純、安価、予備テストに最適。
Non-probability sampling procedures
Quota samapling(割り当て法)
標本の構成は、決まった基準に応じてあらかじめ与えられる。
そしてその基準で自由に選択できる。
Purposive sampling(有意抽出法)
調査基準の観点から、最も重要なタイプが標本に含まれる。
Snowball sampling(雪だるま式抽出法)
数人の選ばれた個人が調査用紙を知り合いの輪の中で次々に渡していく。
例:アンケートを取ったピアニストの知り合いのピアニストを次の調査対象とする
Voluntary sampling(応募法)
1936年の米国での大統領選の例
1916年から大統領選の結果を的中させてきた Literary Digest という雑誌が、240万人のサンプルを対象に以下の数字を挙げた。
また、Gallup という新しく設立された調査会社は、選挙の予測に5万人のサンプル、Digenst の結果予測に3千人のサンプルを対象とした。
選挙戦の結果、ルーズベルトは62%の得票率だったが、両会社ともその数字から乖離があった。なぜであろうか。
⇔ この標本は代表標本ではなかったということ
⇔ データ抽出が無作為とはいえない状況だった
Digest 社:
アンケートを1000万人(!!)へ送付したが、これは電話帳と紳士クラブというリストをもとにされた対象者であった。(1936年に電話を持っている人は全く一般的でない)
これにより、下流層の人々は選別されていた。(selection bias:選択バイアス)
Gallup 社:
Digest 社の予測に対しては、3千名を電話帳と紳士クラブのリストから抽出。
(43%と44%でわずかに1%ポイントの誤差)
選挙予測に対しては割り当て法(Quota sampling)を使用。
6%ポイントの違いがあることから、これも無作為抽出法とは言えない。
1948年の米国での大統領選の例
Public opinion research(1948)
トルーマンとデューイの Gallup 社の予測は44%と50%。
選挙結果は50%と45%。
調査割り当てのエラー:
調査者は自由に割り当てを決められた。
→その人にとって集めやすい共和党員から調査対象を選んだ
※ デューイは共和党候補
1936年~48年の共和党員を通しての調査結果数字は以下。
これ以降はだいたい9週目の内容となる。
9週目は春休みあけ一発目ということもあり、5人しか出席者がいなかった。
ちなみに経済学が嫌われていることは以前書いたが、どうも統計学の期末試験の方が心配な生徒が多いようだ。
統計で隣に座るベトナムの女の子は「あなたは元エンジニアだからいいかもだけどさ」と捨て台詞を言われたし、ハンガリー語のクラスで隣になった女の子は、「経済学も難しいけど統計学が心配だわ~」と言っていた。
確かに9週目の内容、以下に記載する式などは初めて統計をやる者にとっては結構きついかもしれない。専門用語も意味わからんだろうし。(私もわからない)
Questions to be answered
どうやってサンプルから、全体のパラメータまで推測するか。
Statistical inferences
Estimation theory
サンプルに基づいて母集団の特性のおおよその値を決定
次の2つの方法を学ぶ。
point estimation(点推定):単一値の決定
interval estimation(区間推定):調査する特性が最も含まれていそうな間隔で定義
Hypothesis testing(仮説検定)
母集団についての特性がサンプルによって支持されているかどうか判定
Sample characteristics
標本要素とそれらから計算された特性は変動の対象となる。
無作為抽出(random sampling)の場合、サンプル要素とそれらの統計指標は確率変数(random variables)である。
・確立を持つ結果
・結果の分布(形成)はいわゆる標本分布(sampling distribution)
Estimation theory
Estimating function(推定関数)
母集団特性を近似(推定)する標本からの観測値(y1, …, yn)の関数
Expectations
推定関数の値は標本特性(平均)あたりで変動する → unbiased
変動の程度はできるだけ小さくすべき(標準偏差:標準誤差)→ effective
※ 標準偏差:standard deviation、標準誤差:standard error
Selection of the Estimating function
類推の原理:
類推された母集団特性として標本からの同じ指標を計算する。
確率ベースの正確な方法
Point estimation(点推定)
特定の標本から計算された推定関数(estimation function)の値
Population mean estimation(母集団平均推定):sample mean(標本平均)
※ 標本平均を母集団平均とみなす
・unbiased estimate(不偏推定値)
・standard error(標準誤差)
(標本平均の標準偏差:standard deviation of the sample mean σ/√n)
※ この式の証明は講義では取り上げられない
ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー
このままだとわけがわからないので、例題をはさむ。
The average calculated from a sample of 49 items was 250, from which the average deviation of the sample items was 56. What is the standard error of the mean?
標本数 = 49、標本の標準偏差 = 56、標本平均 = 250から、標準誤差は、
σ / √n = 56 / √49
= 56 / 7
= 8
※ 問題文の'average'が引っ掛かるが、割り切って対応する
We took a sample of 70 elements from a population whose standard deviation is 44 for the purpose of average estimation. The average of the sample became 231. What is the standard error of the sample mean (to 2 decimal places)?
標本数 = 70、母標準偏差 = 44、標本平均 = 231から、標準誤差は、
σ / √n = 44 / √70
= 5.25901
2 decimal places なので、
= 5.26
The standard deviation of a population is 24.2. In the case of samples with how many elements, is it true that the average deviation of the sample means from the population mean is 2.2?
母標準偏差 = 24.2、標本平均の標準偏差(標準誤差)= 2.2になるには標本要素数はいくらかと聞かれているので、
σ / √n = 24.2/ √n
= 2.2 ということ。
24.2 / 2.2 = √n
n = 11^2
= 121
We would like to estimate the average monthly income of employed Hungarians from a sample of 1,000 people. The uncorrected standard deviation of the sample is HUF 90,000. What is the value of the standard error (to 1 decimal place)?
標本数 = 1,000、未補正標本標準偏差 = 90,000から、標準誤差は、
σ / √( n - 1 ) = 90,000/ √999
= 2847.47
1 decimal place なので、
= 2847.5
※ 未補正値のため、不偏推定用調整で分母 n を n-1 にする
ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー
Population proportion estimation(母比率推定):sample proportion(標本比率)
・unbiased estimate(不偏推定値)
・standard error(標準誤差)
(標本比率の標準偏差:standard deviation of sample proportion
ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー
ここも例題をはさむ。
In a random sample with 1,336 elements, 933 people were right-handed. What is the standard error of the proportion of right-handed people (to 3 decimal places)?
無作為標本数 = 1,336、そのうち933人が右利き、右利きの割合の標本誤差は、
P = 933/1,336 = 0.69835
0.69835 x ( 1 - 0.69835 ) / 1,336 = 0.00016
これの平方根なので、
√0.00016 = 0.01256
3 decimal places なので、
= 0.013
ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー
Estimation of population standard deviation(母集団標準偏差)
the sample standard deviation (s*)(標本標準偏差)は母集団標準偏差の近辺で変動しない。 → biased estimate(偏った推定値:不偏ではない)
→ 補正:
※ エクセル式は STDEV.S()
※ 式の証明は日本から持参した教科書にあるが、ここでは上記の式を覚えるのみ
ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー
ここもわけがわからないので、例題をはさむ。
From a sample with 53 elements, we determined the variance of the sample elements, for which we obtained the value 79. What unbiased estimate of the population standard deviation should we give (accurate to 2 decimal places)?
標本数 = 53、標本のばらつき = 79から、母標準偏差の不偏推定値は、
s* x √n / √(n - 1) = √79 x √53 / √52
= 8.97325
2 decimal places なので、
= 8.97
From a sample with 48 elements, we determined the variance of the sample elements, which turned out to be 64. What unbiased estimate of the population standard deviation should we give (accurate to 2 decimal places)?
標本数 = 48、標本のばらつき = 64、母標準偏差の不偏推定値は、
s* x √n / √(n - 1) = √64 x √48 / √47
= 8.08466
2 decimal places なので、
= 8.08
ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー
Sampling distribution(標本分布)
・無作為抽出(random sampling)の場合、サンプル要素とそれらの統計指標は確率変数(random variables)
・標本特性の分布(形成)はいわゆる標本分布(sampling distribution)
サイコロの例:
通常のサイコロ4個、出目の平均 → 対称分布(symmetrical distribution)
通常のサイコロ28個、出目の平均 → ≈正規分布(normal distribution)
非対称(小さい方が有利)サイコロ4個 → 右偏分布(right-skewed distribution)
非対称(小さい方が有利)サイコロ28個 → ≈正規分布(normal distribution)
通常のサイコロ4個、1が出る回数 → 右偏分布(right-skewed distribution)
通常のサイコロ28個、1が出る回数 → ≈正規分布(normal distribution)
ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー ー
※ 補足:中心極限定理(Central Limit Theorem, CLT)
母集団の分布がどのような形であっても、標本サイズが大きくなると標本平均の分布は正規分布に近づく。
実際の応用として、世論調査や品質管理などで、標本データから母集団の特性を推定する際に利用される。
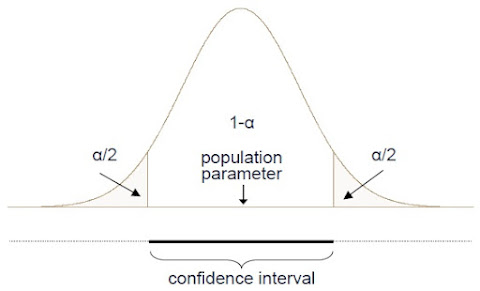
Interval estimation(区間推定)
Confidence interval(信頼区間)
既定の高確率(a predetermined high probability)と共に未知の母集団特性を含む区間
Confidence level(信頼水準)
区間推定(interval estimation)は点推定(point estimation)より前提条件が必要。
母集団分布も知る必要がある。
標本数が多い場合、平均や割合など、いくつかの特性は、母集団の分布に関わらず、正規分布に従う。(すべてのパラメータではない 例:標準偏差)
Confidence interval for mean and proportion
信頼区間(confidence interval):
点推定(point estimation ± 標本誤差(sampling error)
標本誤差(sampling error):
信頼性係数(reliability factor)x 標準誤差(standard error)
あとのスライドの続きは、ハンガリーの市長選を例にした仮説検定の例だが、セミナー中説明されたわけでもないので、今後取り上げられるようであれば、後日追加する。
下記の教科書には、どうして上述の式になるかまで説明されている。
これは私が工学部に在籍していた頃使用していたもので、日本から持ってきて9週目にして初めて役にたった。
 | 新品価格 |







 )
)







0 件のコメント:
コメントを投稿